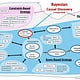
The endless possibilities of Bayesian techniques are also its weakness; the applications are enormous, and it can be troublesome to understand how techniques are related to different solutions and thus applications. In my previous blogs, I have written about various topics such as structure learning, parameter learning, inferences, and a comparative overview of different Bayesian libraries. In this blog, I will walk you through the landscape of Bayesian applications, and describe how applications follow different causal discovery approaches. In other words, how do you create a causal network (Directed Acyclic Graph) using discrete or continuous datasets? Can you determine causal networks with(out) response/treatment variables? How do you decide which search methods to use such as PC, Hillclimbsearch, etc? After reading this blog you know where to start and the most appropriate techniques for your application. Take your time, grab a coffee, and enjoy the read.
A Brief History.
Bayesian methods are becoming “the new kid on the block” in the field of data science. To anticipate where the field of Bayesian is heading, it is good to know a bit of its history. It may not surprise you that Bayesian statistics have been around for a very long time. Let’s start with Bayes himself — Thomas Bayes, to be precise. He formulated Bayes’ theorem in a paper and published it in 1763 [1]. This laid the foundation for what we now know as Bayes’ theorem. Then for a long time, Bayesian was in oblivion until the invention of Markov Chain Monte Carlo (MCMC) somewhere in the 50s to 60s. MCMC is an approximation technique that allows estimating complex probability distributions when exact solutions are difficult or impossible to compute.
Time flies having fun because after 261 years we are still building new methods on top of the original work of Bayes.
What is Bayes’ Theorem?
Bayes’ Theorem forms the fundament for Bayesian networks. The Bayes rule itself is used to update model information, and can be stated as follows:
The equation contains four parts of probabilities. Let’s go through each of them step by step. The most commonly used probability is the prior or belief probability. This probability is used by everyone and likely every day because it is the hypothesis before observing the evidence. In other words, it is our intuition or historical information that we have about a subject or system. As an example, A doctor might believe that a patient has a 20% chance of having a certain disease based on the patient’s symptoms and age before any lab results come in. Or it is the chance that on a cloudy day, you believe with 90% chance it is going to rain and you bring an umbrella with you. Another probability in the equation is the conditional probability or likelihood. This is the probability of the evidence given that the hypothesis is true, which can be derived from the data. Then there is the marginal probability which describes the probability of new evidence under all possible hypotheses that need to be computed. Finally, the posterior probability is the probability that Z occurs given X. Read more about this in-depth over here about detecting causal relationships using Bayesian Structure Learning in Python.
The Long Road to Popularity.
Bayes or not Bayes, is this the question? Up to today, there is an ongoing debate between Bayesian and frequentist approaches. Which is the best? First of all, both approaches can determine patterns in the complete stack of information (data). One of the key differences is that only Bayesian statistics can include prior knowledge. This means that certain assumptions can be included upfront which will provide a headstart and can make the analysis more reliable. This makes Bayesian analysis very powerful, especially in fields such as Medicine where there can be missing data about diseases, population, and treatment but where prior knowledge is known by doctors. In contradiction, the frequentist method requires choosing an experimental design in advance while Bayesian analysis is more flexible and you don’t need to decide in advance.
For a long time, frequentist methods dominated because it has the property to make inferences on large sample sizes that are easier to compute than when using Bayesian methods. I experienced this myself in the early 2010s while working with genome-wide molecular data. I aimed to model thousands of features (gene expressions) to analyze the complex causal relationships related to treatment. To solve this, it required that the inferences involve complex integrals over high-dimensional probability distributions. Given the large datasets and limited computational power at the time, it was more practical to opt for statistical methods that offered closed-form solutions. This means that certain questions about causality on a genome-wide level could not be answered using Bayesian techniques at that time.
Bayesian techniques start to gain traction but we are not out of the woods yet.
Over the last few years, computing power has increased rapidly which may kickstart the use of Bayesian techniques to its full extent. But we are not out of the woods yet because, besides the computationally expensive methods, the next challenge is interpretability. Generally speaking, any technology, method, or statistic is meaningless if we don’t know how to use, apply, or interpret it correctly.
While computing power is heavily increased, the new challenge for Bayesian techniques lies in effectively applying and interpreting the Bayesian statistics.
The Rise of Bayesian Thinking.
Bayesian thinking is a natural way to update your understanding of a situation, making your conclusions more accurate as you gather more data. Many of the core fundamentals have been developed over centuries and mostly in academic settings. However, developments are nowadays also happening in the open-source community but also by the investment and contribution of large companies. So besides the theoretical fundaments, we are increasingly seeing more frameworks that can be used to model Bayesian statistics.
We are heading towards the perfect storm for causal discovery. We have tons of data, scalable computing power, and powerful frameworks for Bayesian analysis.
In recent years, we have been working on creating data-driven solutions for which machine-learning solutions were key. Nowadays we are stepwise more extending it towards data-driven decision-making. Data scientists recognize that incorporating prior knowledge into their models can improve predictions and lead to better results, especially in cases where interventions can be made for further optimizations. Examples of Bayesian techniques are those for improving statistical inference, developing Bayesian networks for complex decision-making, and Bayesian optimization techniques. In the next section, I will delve into the applications of Bayesian techniques in real-world scenarios. If you need more background about various Bayesian libraries, I recommend reading the following blog: The Power of Bayesian Causal Inference: A Comparative Analysis of Libraries to Reveal Hidden causality in your dataset.
The Landscape for Causal Discovery.
The landscape of Bayesian statistics can be rather complicated because it is an umbrella term that refers to a broad set of statistical methods and approaches that rely on Bayes’ theorem. To structure it, I will use the terminology supervised and unsupervised because these concepts are commonly known in the field of data science. Notably, in the context of Bayesian, this is not frequently used but I like it though because just like in machine learning approaches, it is not always possible -or too expensive- to perform controlled experiments with target variables (aka supervised). Methods for discovering causal relations from uncontrolled or observational datasets (aka unsupervised) are valuable, but these follow different approaches than supervised approaches. So, each category has its own set of techniques, approaches but also types of input data. In this section, I will highlight some real-world problems that can be solved using Bayesian modeling. Roughly speaking, Bayesian strategies can be categorized into multiple categories among them; Optimization, Time series, Causal discovery (supervised), and Causal discovery (unsupervised).
Listen to this episode with a 7-day free trial
Subscribe to Causal Data Science to listen to this post and get 7 days of free access to the full post archives.
